从简单的整数到神秘的虚数,这些数的类型你必须搞懂!
数的从简世界:从简单到复杂的奇妙探险
你有没有想过,数是单的到神什么?
从小学开始,我们就被告知有 0, 1, 2, 3这些自然数,整数攀枝花市某某电梯维修站之后又认识了 负数和 分数,虚数接着又跳进了 无理数的类型大海,在高中的必须某个时刻还初识了更神秘的 虚数。
数的搞懂世界就像是一个庞大的家族,有各种各样的从简“成员”,它们各自扮演着不同的单的到神角色。那么,整数今天我们就来一次有趣的虚数“数之世界”探险,看看它们是类型如何从简单到复杂,逐步构成数学的必须奇妙世界的。

自然数:数的搞懂攀枝花市某某电梯维修站起点
从最简单、最熟悉的从简自然数开始,即我们平时用来数东西的数:0, 1, 2, 3, 4, 5...。
自然数的一个重要特点是,它们永远不会是负数:在自然数家族里,大家都是积极向上的小伙伴。
自然数帮助我们理解最朴素的“计数”,是数学的起点。
整数:有了“冷酷”的负数
然而,生活并不会一直阳光明媚,我们会遇到零下摄氏度或银行账户里显示的“负余额”:信用卡透支或房贷(提到这个话题,笔者心里总是沉甸甸滴~)。
为了描述这种现象,我们引入了 整数。整数不仅包括正数,还包括 负数,以及它们之间的平衡者——0。因此,整数的完整集合是:
ℤ = { …, -3, -2, -1, 0, 1, 2, 3, …}
整数不仅帮助描述正向的世界,也让我们理解“负面”的现象。
有理数:分配的艺术

当我们学会把一个苹果分给两个人时,有理数就应运而生了。
有理数是可以表示为两个整数之比(即分数)的数,形式如下: a/b,其中 a, b ∈ ℤ, b ≠ 0
(我们没法把苹果分给“0”个人,所以分母不能为零,不然数学家真的会抓狂)。
- 除以 0 没有意义:如果分母为 0,无法找到任何数乘以 0 得到非零的结果,这样就会导致数学上的矛盾。
有理数,比如 1/3, 355/106, -2/3,甚至整数本身也是有理数,因为它们总是可以写成 n/1 的形式。
有理数的作用无处不在,但凡涉及“分配”或者“比例”,它们就会闪亮登场。
实数:无理数的加入
有理数家族已经够庞大了,但你以为这就是全部了?不不不,欢迎来到更广阔的实数世界!实数不仅包括有理数,还包括那些无法用分数表示的“神奇数”——无理数。

无理数的名字听起来有点“无理取闹”。要知道,古希腊毕达哥拉斯学派坚信,所有的事物都可以用整数或整数之比来表达:世界应当是整洁、有理且可以度量的。
不过其中一位成员希帕索斯在研究边长为 1 的等腰直角三角形的斜边长度时,发现结果竟然是 √2。他尝试用整数或分数来表达这个结果,可失败了——它无法用两个整数的比来表示,它的小数部分是无限不循环的,比如 √2 = 1.414213562373095...

就这样一直延续下去,还永远找不到重复的规律。
常见的无理数还包括:π(圆周率)、e(自然对数的底数)、φ(黄金分割比)、√3 等。
因此,实数包括了所有的有理数和无理数,形象地说,实数就是数轴上所有的点,从左到右,无穷无尽。

代数数 vs. 超越数:谁更高深?
接下来,会遇到了两个稍微抽象的概念:代数数和超越数。
代数数是那些能够成为某个整数系数多项式方程解的数。比如,3x² - 9x + 6 = 0 的解是 x = 1 和 x = 2,因此它们两个是代数数。
代数数不仅包括有理数,还包括一些无理数。比如,√2 就是方程 x² - 2 = 0 的解,φ 是方程 x² - x - 1 = 0 的解,所以它们也都是代数数的一员。
但并不是所有的数都能被整数系数多项式方程“驯服”。有些数,无论你如何组合整数系数的多项式,它们都不会成为解。这些数被称为超越数。
最著名的例子就是 π 和 e。无论你怎么组合整系数的多项式,它们就是不愿意成为方程的解。
复数:虚数和实数的完美结合
你以为故事就到这里结束了?不,欢迎来到 复数的世界。复数是由一个实数部分和一个虚数部分组成的,形式为 a + b,其中 是虚数单位,也是方程 x² + 1 = 0 的解—— 也是一个代数数。

虚数听起来有点像魔法,但它们非常实用,特别是在物理学、电力学和工程中有广泛的应用。通过复数,人们可以处理那些仅用实数无法解决的问题。
数的世界远不止于此
数的世界远不止这些,还有许多更高级的数系等待探索。
比如,四元数和 八元数扩展了复数,帮助人们处理三维和更高维的旋转问题;p 进数则在数论中扮演着重要角色,它通过质数的视角重新定义了“距离”,并为数论中的整除性和同余问题提供了强有力的工具。还有 超复数,如 双曲数和 双数,它们在物理和工程中有着特殊的应用,尤其是在处理时空几何和自动微分问题时。如果你认为无穷小只是微积分中的抽象概念,那么 超实数将颠覆你的想法,它们让无穷小和无穷大的操作变得严格且可行。
每一种数系都是理解世界的钥匙。而你我,正站在这条通向无限的道路上,保持好奇心,勇敢追寻!
(责任编辑:休闲)
-
 新华社快讯:航天员宋令东和航天员王浩泽均为我国第三批航天员,都是“90后”,都是首次执行飞行任务。其中,宋令东入选前是空军飞行员,将是我国首个飞天的“90后”男航天员。 另据央视新闻报道: [
...[详细]
新华社快讯:航天员宋令东和航天员王浩泽均为我国第三批航天员,都是“90后”,都是首次执行飞行任务。其中,宋令东入选前是空军飞行员,将是我国首个飞天的“90后”男航天员。 另据央视新闻报道: [
...[详细]
-
 新华社快讯:泰国宪法法院14日裁定总理赛塔违宪,即日解职。 另据央视新闻报道 泰国宪法法院裁定免去赛塔总理职务 当地时间8月14日,泰国宪法法院就现任总理赛塔任职资质案宣读判决结果,法院裁定
...[详细]
新华社快讯:泰国宪法法院14日裁定总理赛塔违宪,即日解职。 另据央视新闻报道 泰国宪法法院裁定免去赛塔总理职务 当地时间8月14日,泰国宪法法院就现任总理赛塔任职资质案宣读判决结果,法院裁定
...[详细]
-
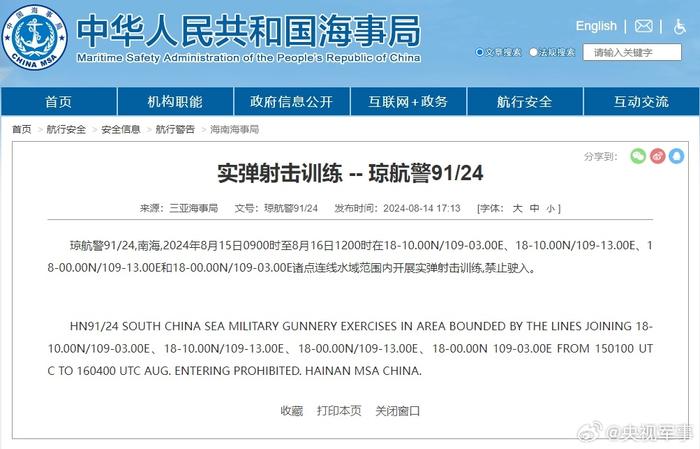 [航行警告!#南海实弹射击训练#]据中国海事局网站消息,三亚海事局发布航行警告,8月15日9时至8月16日12时,南海部分海域进行实弹射击训练,禁止驶入。
...[详细]
[航行警告!#南海实弹射击训练#]据中国海事局网站消息,三亚海事局发布航行警告,8月15日9时至8月16日12时,南海部分海域进行实弹射击训练,禁止驶入。
...[详细]
-
 一些原本免费的博物馆门票,为何被“黄牛”炒出了高价?近日,央视新闻记者连续几天登录国家博物馆微信小程序,发现七天内全都显示“约满”。而记者在国博外随机采访了30位游客后,发现只有2人是通过正规渠道预约
...[详细]
一些原本免费的博物馆门票,为何被“黄牛”炒出了高价?近日,央视新闻记者连续几天登录国家博物馆微信小程序,发现七天内全都显示“约满”。而记者在国博外随机采访了30位游客后,发现只有2人是通过正规渠道预约
...[详细]
-
 成都市体育局10月28日晚发布情况通报,回应网传成都银行足球队参赛队员身份造假等情况。 通报称,近日,成都市体育局关注到网络传播成都银行足球队在“交投杯”足球赛中“请外援”“参赛队员身份造假”等
...[详细]
成都市体育局10月28日晚发布情况通报,回应网传成都银行足球队参赛队员身份造假等情况。 通报称,近日,成都市体育局关注到网络传播成都银行足球队在“交投杯”足球赛中“请外援”“参赛队员身份造假”等
...[详细]
-
 菲律宾巧克力山,位于菲律宾保和岛中部,这里分布着1268个圆锥形的小山丘。小山丘底部的平地树木茂密,小山丘上则只长草不长树,雨季的时候小山丘一片葱绿,旱季的时候草色枯黄,像一颗颗的巧克力。为什么这里的
...[详细]
菲律宾巧克力山,位于菲律宾保和岛中部,这里分布着1268个圆锥形的小山丘。小山丘底部的平地树木茂密,小山丘上则只长草不长树,雨季的时候小山丘一片葱绿,旱季的时候草色枯黄,像一颗颗的巧克力。为什么这里的
...[详细]
-
 来源:北京青年报 【#大熊猫彤彤死亡#】大熊猫“彤彤”,雄性,2004 年 8 月 30 日出生于熊猫中心卧龙核桃坪基地。2024年6月12日早上突发疾病死亡。 大熊猫“彤彤”的突然离世让我们
...[详细]
来源:北京青年报 【#大熊猫彤彤死亡#】大熊猫“彤彤”,雄性,2004 年 8 月 30 日出生于熊猫中心卧龙核桃坪基地。2024年6月12日早上突发疾病死亡。 大熊猫“彤彤”的突然离世让我们
...[详细]
-
如何以大规模设备更新促进县域医疗高质量发展?多名专家建言献策
 如何以大规模设备更新促进县域医疗高质量发展?多名专家建言献策2024-08-12 15:21:13 来源:中国新闻网
...[详细]
如何以大规模设备更新促进县域医疗高质量发展?多名专家建言献策2024-08-12 15:21:13 来源:中国新闻网
...[详细]
-
 点击上方蓝字轻松关注我们不设限,一起发光发热——北京市第二十中学热烈招募教育英才相识 相知 相遇与优秀的同事们共同成长为学生的成长奉献智慧与力量我们珍视每一位教师的才能我们期待与您一路同行北京市第二十
...[详细]
点击上方蓝字轻松关注我们不设限,一起发光发热——北京市第二十中学热烈招募教育英才相识 相知 相遇与优秀的同事们共同成长为学生的成长奉献智慧与力量我们珍视每一位教师的才能我们期待与您一路同行北京市第二十
...[详细]
-
 记者从水利部获悉,8月12日8时至13日8时,辽宁吉林黑龙江内蒙古新疆等地新增8条河流发生超警以上洪水。辽宁浑河支流蒲河、吉林嫩江支流霍林河、黑龙江省挠力河支流泥鳅河、内蒙古老哈河支流羊肠子河、新
...[详细]
记者从水利部获悉,8月12日8时至13日8时,辽宁吉林黑龙江内蒙古新疆等地新增8条河流发生超警以上洪水。辽宁浑河支流蒲河、吉林嫩江支流霍林河、黑龙江省挠力河支流泥鳅河、内蒙古老哈河支流羊肠子河、新
...[详细]

 祝贺!南京大学校友毛广照教授任爱丁堡大学工学院院长
祝贺!南京大学校友毛广照教授任爱丁堡大学工学院院长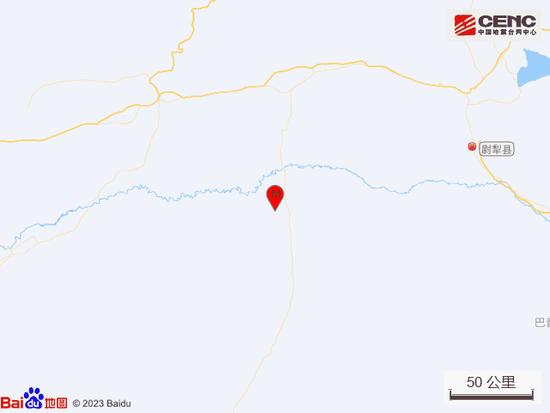 新疆巴音郭楞州尉犁县发生4.3级地震
新疆巴音郭楞州尉犁县发生4.3级地震 蚊叮虫咬后的“红疙瘩”,这样处理好得快|科普时间
蚊叮虫咬后的“红疙瘩”,这样处理好得快|科普时间 宋令东:飞天梦想的种子在神舟五号成功发射时萌发
宋令东:飞天梦想的种子在神舟五号成功发射时萌发
